The Law of Structure in Fuller’s Halo Essay
- Dante Michael
- 24 hours ago
- 9 min read
Updated: 1 minute ago

Buckminster Fuller’s essay “Omnidirectional Halo” was presented to the International Union of Architects at their 1965 World Congress. I can’t imagine that it hit the mark with his audience. Even today, the Halo essay defies summarization. Packed into 9000 words are concepts as far-ranging as the Doppler effect, relativity, entropy, infinity, omniscience and omnipotence. Tables of geometrical calculations only complicate matters, especially for anyone new to Fuller.
To keep things simple, I will focus on a single aspect of the Halo essay: “The Law of Structure”. This is a brief review of the philosophically relevant issues in the Halo essay: inductive reasoning and Fuller's knowledge claim of 'a priori geometry'. The essay’s Introduction offers a relatively clear picture of its aim. Even with abridgements, it’s a mouthful:
“A total epistemological reorientation and, to the best of my knowledge, a unique philosophical reconceptioning… seem to have followed gradually upon my hypothetically-initiated querying… regarding dawningly apparent natural laws.”
This essay is about epistemology - “the science of the thinking processes”. Fuller claims to have made a discovery by means of a hypothetical investigation of natural laws. This method proceeds by induction, moving from particular observations to generalized principles or ‘laws’. Although Fuller never refers to induction specifically, he depicts it using the analogy of file cards:
…a pack of one hundred 4-inch by 5-inch file cards each riddled with hundreds of different sized small holes. …when the cards are stacked with edges aligned three holes in each card are vertically aligned; all others are obscured by blank spaces on one card or another. A triangular pattern relationship of the light coming through three tubes in the stack of cards is now lucidly conceptual…. We may apply the term “pattern generalization”.
Every card has hundreds of holes in seemingly random spots. If we consider each card to be a particular observation or experience of one kind or another, then the stacking of cards is analogous to inductive reasoning. We check each special case against the rest to see what holds in all cases. In this analogy, inductions are confirmed visually. We can ‘see’ that every card is always punched in three fixed locations. This is how laws or principles are discovered.
There is an obvious objection here: what if a card comes along that blocks the pattern? What if a new observation contradicts the generalization? Conceiving this possibility as a persistent threat, are we ever justified in believing that every future card will resemble the cards that are already stacked? This problem of induction has occupied modern philosophers since the Early Modern period and is difficult to solve without circular reasoning. The only justification for an induction appears to be… another induction. Ideally, we would use deduction to confirm a certain conclusion rather than settle for a merely probable one. But let’s continue with Fuller’s file cards.
He differentiates between first and second-order generalizations that emerge from the “co-ordinate consideration of a plurality of generalized conceptual principles”. I can offer my own explanation for this section (paragraphs 3-5 of the Introduction). Suppose that all of our file cards are coloured red, green or blue. We stack the cards according to their colour, revealing colour-specific patterns (these are ‘first-order’). Now suppose that we start mixing the cards systematically: one red card in front of green, one green in front of blue and so on. We are checking for what holds across all cards regardless of colour.
If we stick with the triangular pattern from earlier, then the second-order pattern is simple enough to imagine. Any two colours will show only two holes instead of three (the hole not in common is what distinguishes the first-order patterns of each colour). But when all three colours are stacked together, only one hole can be seen - the one that all three colours share. Indeed, this operation is more complex than the first-order case since we had to compare ‘kinds’ of cards to discover this pattern. It seems that such evidence strengthens the induction itself on the grounds of natural kinds.
Concerning these second-order patterns, Fuller begins to speak of mathematics and predictions:
"When a second order of pattern distillation as a generalized conceptual principle emerges… as to provide a means of mathematical accounting and therefrom a tentative forecasting capability… then we may tentatively assume that we have discovered at least a clause of “natural law”.
Fuller’s caution is appropriate here. It is never beyond the realm of possibility that a new experience may contradict even second-order generalizations. The problem of induction is not so easily overcome! Nonetheless, Fuller is prepared to surmount the ‘tentative clause of natural law’ to proclaim the 'Law of Structure':
"I have found a general law of total synergetical structuring, which we may call The Law of Structure. This law discloses that ‘universe’ of total man experience may not be simultaneously recollected and reconsidered, but may be subdivided into a plurality of locally tuneable event foci or ‘points’ of which a minimum of four positive and four negative points are required as a ‘considerable set’; that is, as a first finite subdivision of universe."
Fuller’s language remains ambiguous. Laws imply necessity of one kind or another and his definition seems to lack confidence. ‘May’ the universe be subdivided or must it be? The only term that is suitably lawlike here is ‘required’; what is required by the Law of Structure? Four positive and four negative points for a considerable set, at minimum.
It’s possible that Fuller had reservations about claiming to have discovered a ‘law’. The phrase ‘Law of Structure’ never appears in Synergetics, which was published about a decade later. Instead Fuller reverts to the earlier 1963 version of the Halo essay, where the Law was replaced by “The Scenario Principle” and then by the “The Principle of Design Co-Variables”. This seems anachronistic and there's some more detective work to be done.

The essay as it appears in the Design Science Decade documents (1965). In 'No More Secondhand God' (1963), the yellow instance reads 'The Scenario Principle' and the red instance 'The Principle of Design Co-Variables". Image courtesy of Benjamin Lowder.
Whether we are dealing with a ‘law’ or a ‘principle’, Fuller insists that his discovery is not an invention. This defensive stance shapes the flow of his rhetoric, combining anecdotes about how he ‘starts with universe’ while subtracting his own psychology from the results of this method. The strategy bears resemblance to Immanuel Kant’s in The Critique of Pure Reason (among other works). Kant (1724-1804) dwelled on the link between human psychology and a priori knowledge, especially our knowledge of geometry. His writing contains tactful descriptions of his inner reflections on these topics, clarifying personal ideas for the reader amidst an otherwise objective account of reason.

I’ll briefly describe Kant’s solution to the problem of induction using Fuller's file card analogy. Kant argued that there are 12 distinct locations for holes on every card. In order for a card to be an ‘object’ of experience, it must have at least some of these holes punched. These necessary punch-spots are known as the Categories. Kant called this a transcendental generalization since it concerns the possibility of experiencing objects in general. This is a remarkable idea because it suggests that we arrive at our knowledge of the categories without looking at any cards, i.e. independently of experience. We justify our inductions of lower-order patterns because we have knowledge of the very ‘laws of understanding’ that make our experience possible (such as causality). This is what a priori knowledge means for Kant. By contrast, an empirical generalization is discovered by examining cards directly (a posteriori).
In the Halo essay, Fuller explicitly claims to have discovered “a priori geometry”. Rather than focus on 'objects of experience' like Kant's transcendental method, this geometry is meant to have direct application within epistemology, i.e. to the ‘thinking processes’. Pushing the limits of the card analogy even further: there must be certain holes punched in every card in order to even have a thought about a card at all. This requirement (like Kant’s categories) is what makes geometry functionally a priori by applying it to any and all “considerable sets”, by necessity, under the Law of Structure. And if this Law turns out to be sufficiently transcendental, then we ought to know it without checking our particular thoughts to determine whether it holds true or not. Try figuring that one out!
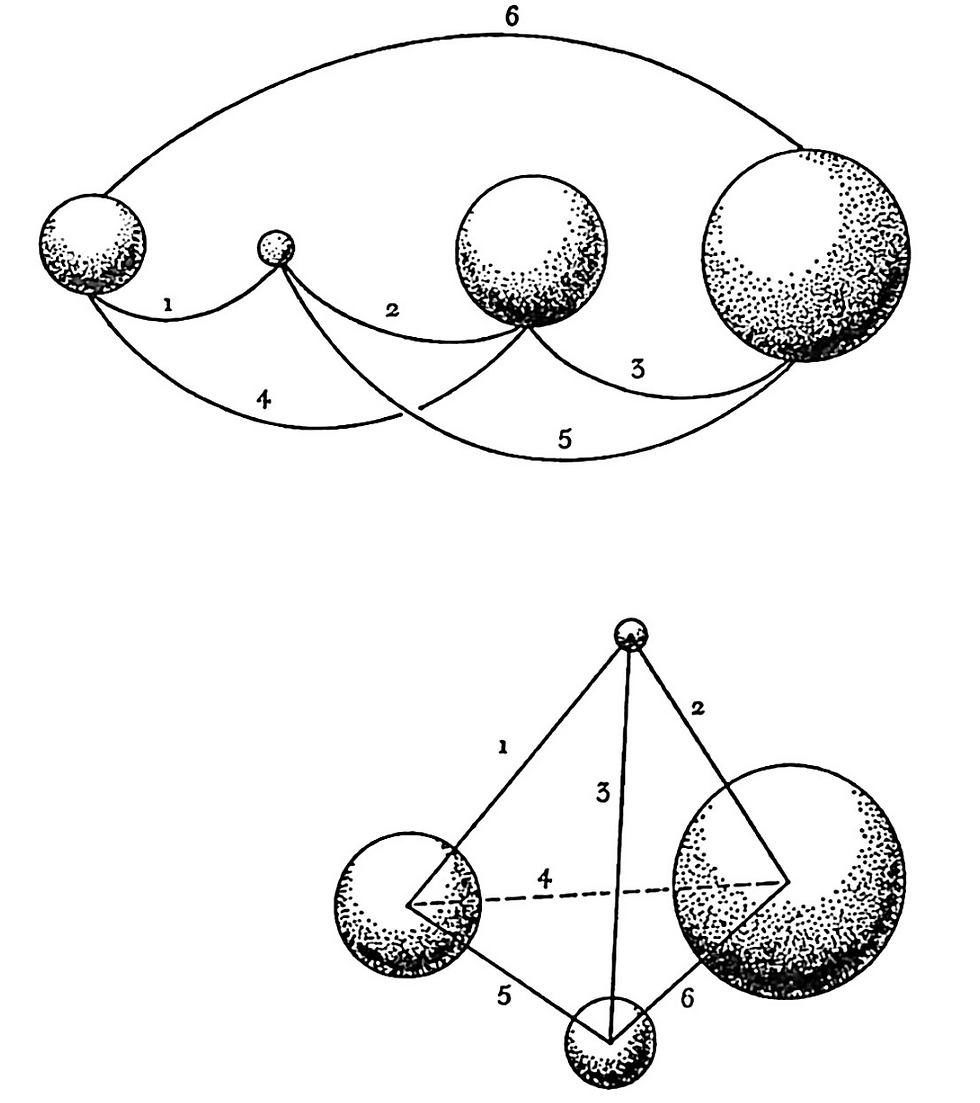
Figure 2 from the Halo essay shows a "Linear Tetrahedron". Four positive (or four negative) foci define a tetrahedron.
Why was Fuller convinced that his geometry was a “unique philosophical reconceptioning” that would reorient epistemology? Perhaps it was the same reason why Kant believed that his Critique of Pure Reason was a Copernican revolution in philosophy (a term he coined). We might admire their confidence but it seems that neither man succeeded in producing their desired effect. Kant’s transcendental deductions, though enormously influential, have never been accepted as he had envisioned they would be. Compare this to the actual Copernican revolution, which reoriented cosmology towards heliocentrism and its associated principles of celestial and terrestrial motion. Kant's critical variety of idealism was meant to facilitate the same reorientation for metaphysics.
A genuine solution to the problem of induction is indistinguishable from a scientific discovery. Induction has only ever been 'solved' by scientists like Kepler, Galileo and Newton; philosophers have only explored what it means for a solution to be offered. Induction is always a demonstration, not just an argument. Fuller walks in Kant's footsteps by claiming objective validity for the Law of Structure while also qualifying it as a priori knowledge, which is non-empirical. He's playing two roles at once - scientist and philosopher, queen and handmaiden. It doesn't seem like a problem until the latter upsets the rule of Science by striking out on her own. "How", writes Kant, "can metaphysics be married to geometry, when it seems easier to mate griffins with horses than to unite transcendental philosophy with geometry?" (Preface to the Physical Monadology, 1756).
What sets Fuller apart from Kant is his use of models. Whether its physical polyhedra or just drawings on a page, Fuller's extensive use of topology has intrinsic value for philosophy. The reason is because of the ostensive reference supplied by the models, which permit definitions by 'pointing'. This is how we learn colours as children, by hearing the word 'yellow' and then having someone point to an appropriate object. Just try to define yellow without pointing to something yellow! Making topology central to his philosophy allows Fuller to show his reasoning in the same way. He called it operational mathematics.
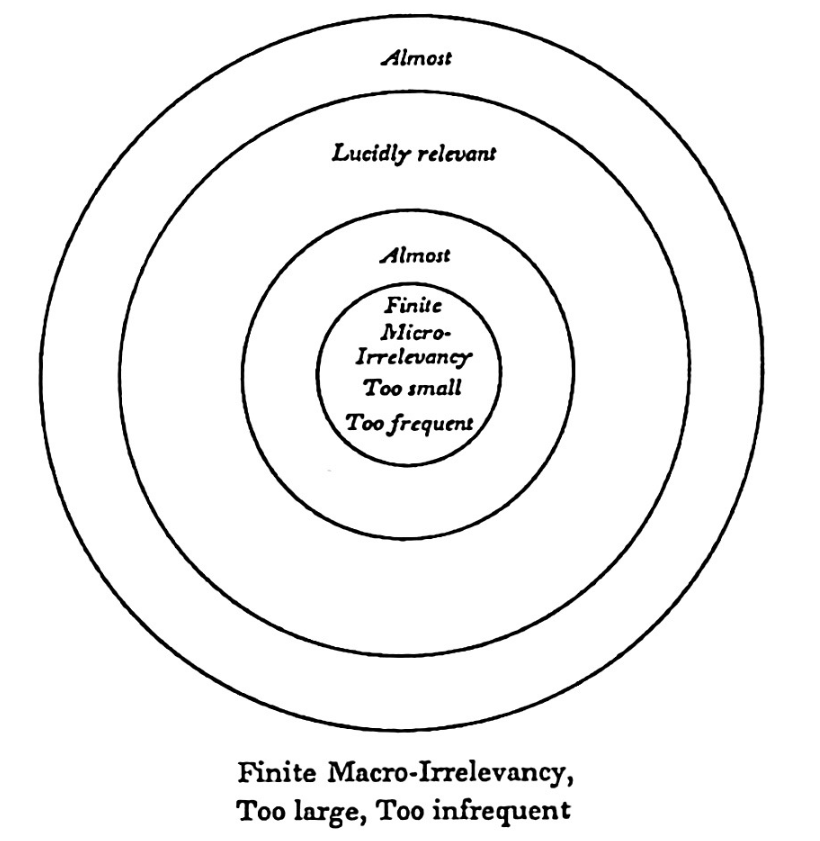
The degree to which ostension strengthens induction is an open and profound question. Giving visible reference to things certainly touches a primal nerve, as if the process were more physiological than cognitive. It strikes me that Fuller wanted to cultivate this primitive response in order to facilitate learning through fundamental (naive) cognition. This would explain why he claimed, quite dogmatically, that ‘thinking has shape’. Perhaps a reflective engagement with this idea will 'shape one's thoughts' accordingly.
The Omnidirectional Halo itself is one of Fuller's simpler models made of four concentric circles (or spheres). Notice that it comprises 5 areas, ranging from the microcosmic, inner concavity to the macrocosmic, outer convexity. These three examples designed by Fuller are Figures 3, 4 and 5 in the Halo essay.
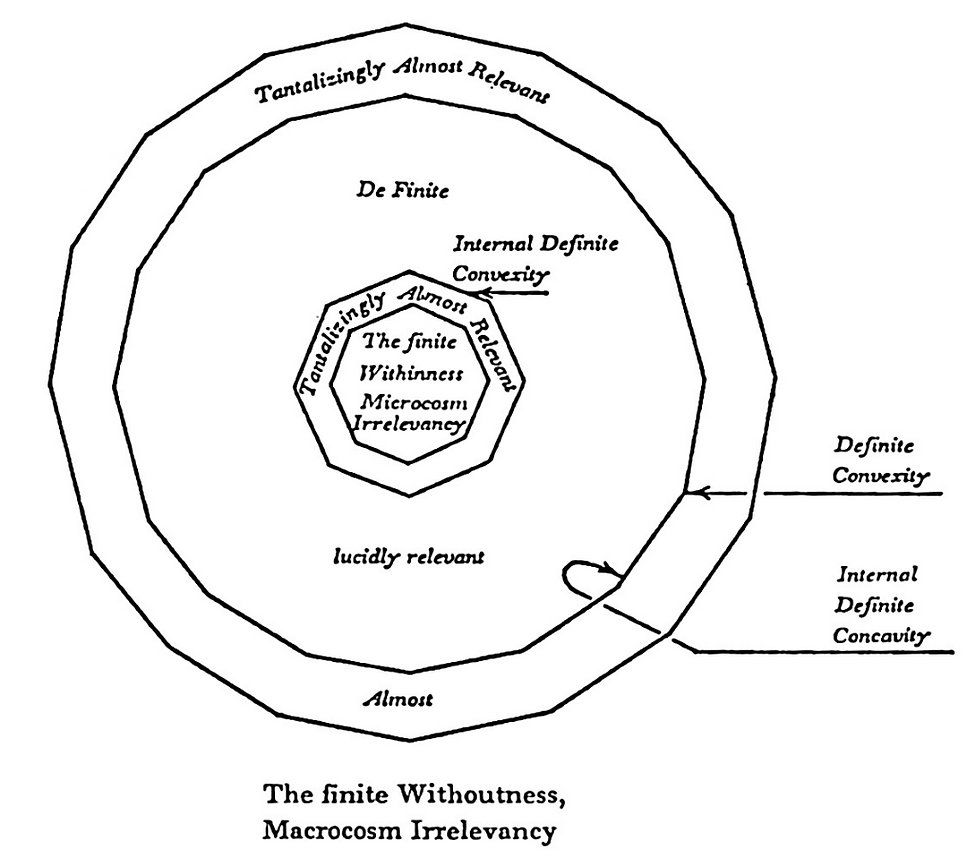
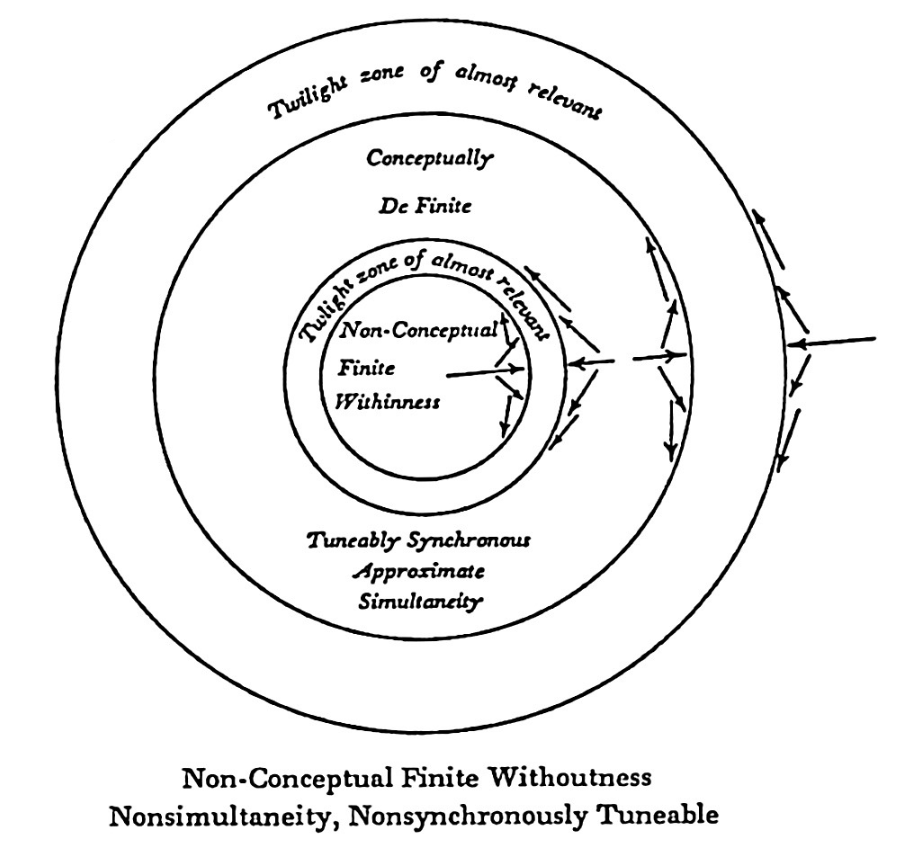
Does the Halo model exhibit the Law of Structure? Surely, yes - the four circles create four positive event foci (the concave areas) as well four negative foci (the complementary, convex areas). This topological identity is consistent with the Law of Structure and is produced by the Halo by necessity. But this mathematical necessity is only a priori knowledge in the trivial sense that all of mathematics and logic is knowable a priori. No - what we seek (and what Fuller wants to show) concerns the apparently contingent model of the Halo itself, its ‘being drawn’ in such a way as to create the pattern now being recognized as a Law of Structure (a drawing is not a proof). Only on the assumption that the Omnidirectional Halo is an accurate model of the first subdivision of Universe, that it really ‘exists’, that it reflects ‘reality’ or belongs to a ‘natural kind’, can we hope to catch a glimpse of the necessity that is significant to epistemology. And only then would we be justified in assiging the a priori predicate to our knowledge of the Law of Structure and its 'synergetic' geometry. That is, of course, if we are willing to throw the 'tentative clause of natural law' out the window.


About the Author:
Dante Diotallevi is an independent scholar living in Canada. He holds a BSc. in Biology and an M.A. in Philosophy from Queen's University in Kingston, Ontario.

























ความคิดเห็น